线段树 | Kyons'Blog 


 




线段树

发表于 | 分类于 | | 阅读次数:

欢迎各大佬，大牛对本文指正，也希望本文能对各位有所帮助

本篇很多地方借鉴英雄哪里出来的博客%%%

一、基本概念

  1. 线段树是一棵二叉搜索树，它储存的是一个区间的信息。
  2. 每个节点以结构体的方式存储，结构体包含以下几个信息：每个节点以结构体的方式存储，结构体包含以下几个信息：

    (1). 区间左端点、右端点

(2). 区间所代表的值

(3). 该节点的子节点

  1. 线段树的基本思想：二分。
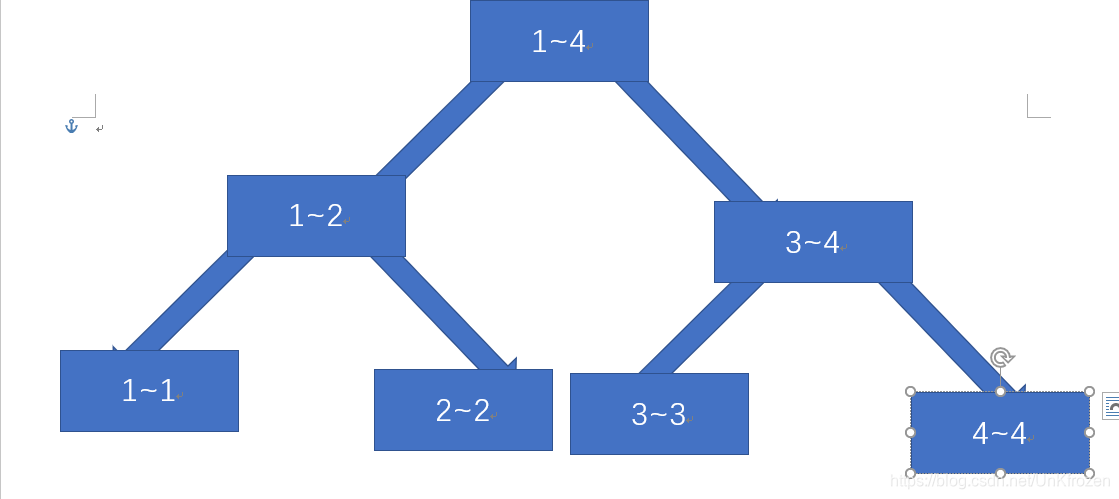
  2. 线段树一般结构如图所示：
    假设数据为4个数，则树应是这样word大法好
    1. 由上图可知，每个节点的

每个节点的左孩子区间范围为[left，mid]，右孩子为[mid+1,right]

二、代码实现与基本操作

0.基础数据结构

1
2
3
4
5
6
7
8
9
#ifndef NULL  //防报错
#define NULL 0
#endif
typedef struct Segment_Tree* Node;
struct Segment_Tree {
    int d;
    int left, right;
    Node lson, rson;
}*root;

1.建树 built函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Node built(int left, int right)
    {
        Node p = new(Segment_Tree);//Node p=(Node) malloc(sizeof(Segment_Tree));,c用法
        //申请一个新内存，并令p指向该处
        p->left = left;     //储存区间信息
        p->right = right;
        if (left == right) {
            p->d = a[left];  //scanf("%d",&p->d),cin>>p->d,皆可，及储存数据
            p->lson = NULL;    //令左儿子和右儿子指向NULL
            p->rson = NULL;
        }
        else {
            int mid = (left + right) / 2;    //二分
            p->lson = built(left, mid);    //左儿子
            p->rson = built(mid + 1, right); //右儿子
            p->d=p->lson->d+p->rson->d;  //存储左儿子和右儿子的和
        } 
        return p; //返回指向该处的指针
}

  除了建树，相应关闭树的函数为：

1
2
3
4
5
6
7
8
9
void close(Node p)
{
    if (p != NULL) {
        close(p->lson);
        close(p->rson);
        delete(p); //free(p);c用法
    }
    return;
}

 非常需要注意的一件事，每次用指针建立树的时候，请务必写一个关闭清理申请的内存的函数

2. 单点查询

  (1).查找k位置的数据

1
2
3
4
5
6
7
8
9
int find(Node p, int k)
{
    if (p->left == p->right&&p->left == k)
        return p->d;
    int mid = (p->left + p->right) / 2;
    if (k <= mid)
        return find(p->lson, k);
    return find(p->rson, k);
}

3.单点修改

  (1).知道点所在位置，修改该点处值

1
2
3
4
5
6
7
8
9
int update(Node p, int x,int k)  //对x位置的值，进行k值的变动
{
    if (p->left == p->right&&p->left == x)  //如过找到了k位置
        return p->d +=k;           //对该点值进行操作，可以为+-*/等
    int mid = (p->left + p->right) / 2; //判断该点在左区间还是右区间
    if (x <= mid)   //如果是左区间，只对左区间进行递归查询
        return p->d = update(p->lson, x, k)+p->rson->d;  //查找完后对父节点存储值进行修改
    return p->d = p->lson->d+update(p->rson, x, k); //不是该点，也不在左区间，只能是右区间
}

4.区间查询

手绘的哦
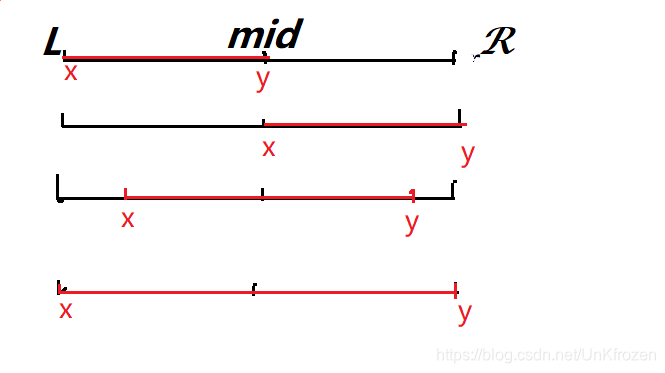
  所给区间仅可能为上图四种情况。
  通过一定操作，我们都可以将上三种，全部转换为最后一种直接输出。
  闲话少说，代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
int find(Node p, int x,int y)  //注，这里假设任意x,y，都有x<y
{
    if (p->left == x && p->right == y)  //如果是第四种情况，直接返回
        return p->d;
    int mid = (p->left + p->right) / 2;   //求中间值
    if (y <= mid)   //如果查询区间在mid左边，因为x<y<=mid
        return find(p->lson, x, y); //那么直接递归左儿子
    if (x > mid)   //如果查询区间在mid右边，因为mid<x<y
        return find(p->rson, x, y);  //那么直接递归右儿子
    return find(p->lson, x, mid)+find(p->rson, mid + 1, y);  //两式都不符合，及x<=mid<y
                            //则从mid为中间值分开
                            //左儿子查询[x,mid],右儿子查询[mid+1,y]
}

5.区间修改

1
2
3
4
5
6
7
8
9
10
11
int update(Node p, int x, int y, int k)  //设区间为[x,y]，修改的值为k
{
    if (p->left == p->right && p->left == x)  //如果是这个区间内的元素，就让它+k
        return p->d+=k;
    int mid = (p->left + p->right) / 2;  //二分
    if (y <= mid)   //如果区间在中值的左侧
        return p->d=update(p->lson, x, y,k)+p->rson->d;  //仅需更新左儿子的值，并更新父亲的值
    if (x > mid) //如果区间在中值的左侧
        return p->d=p->lson->d+update(p->rson, x, y,k); //同上
    return p->d=update(p->lson, x, mid,k) + update(p->rson, mid + 1, y,k); //如果区间被中值分开
}

三.优化

（一）. Lazy-Tag懒标记

  我们考虑一下区间改值的过程：当更改某个区间的值的时候，子区间也跟着更改。显然，在大数据下，这样操作会导致TLE。
  怎么办？
  这时我们就引入一个优化方法，叫做Lazy-Tag懒标记。
  何为懒标记呢？顾名思义，就是用来偷懒的减少修改时消耗时间的。即：
  当我想要对某一区间的所有元素都+k时，在修改该区间节点时，对其打上标记lazy，并记lazy为k，修改该节点的值为+区间长度*k，立刻return，而不将该节点下面的所有子节点一一修改。

思想实现

  如图示：1~4的值分别为1，2，3，4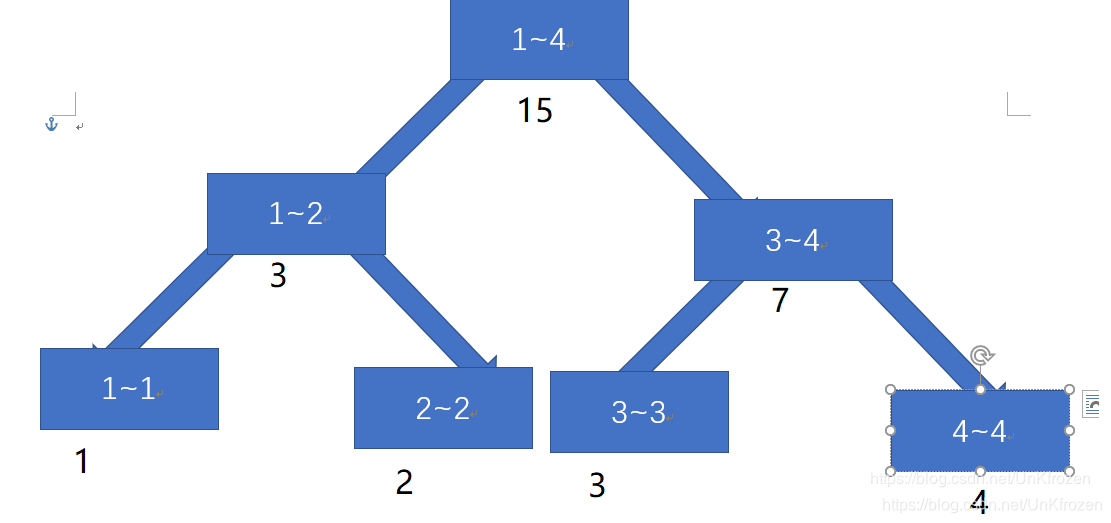
在这里插入图片描述
  我们选择对[1,2]区间进行修改，要求改区间所有值+2，则：在区间[1,2]，打上标记lazy=2，并修改其值为3+(2-1+1)2，直接返回，并不对其子节点进行修改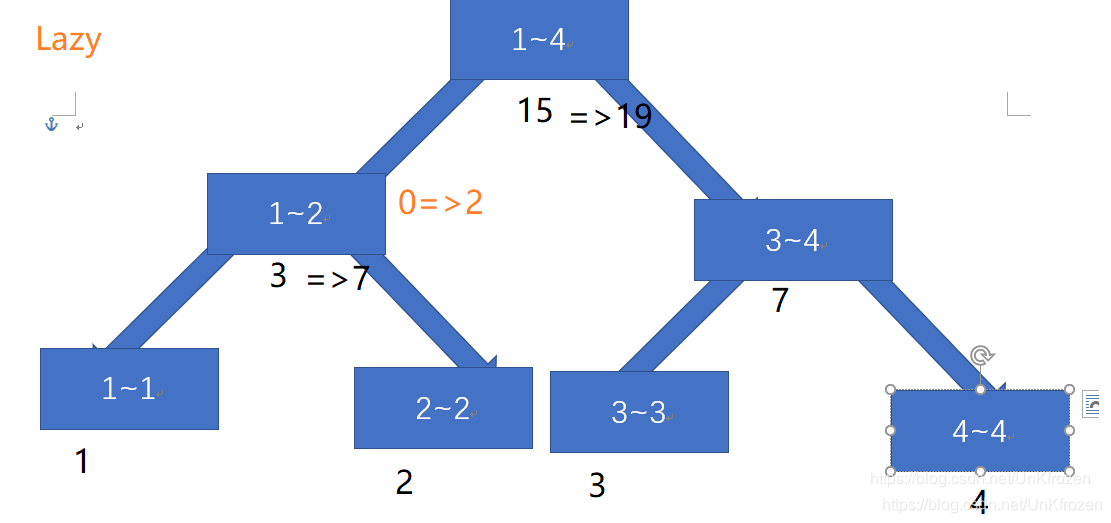
纯手搓！！
  当我们再次对[1,2]区间修改时，并要求区间内所有的值+1，则：由于[1,2]有标记lazy=2，于是我们将lazy标记向其子节点传导，并修改其子节点的值。再在[1,2]区间打上lazy=1，修改值为(2-1+1)1，返回。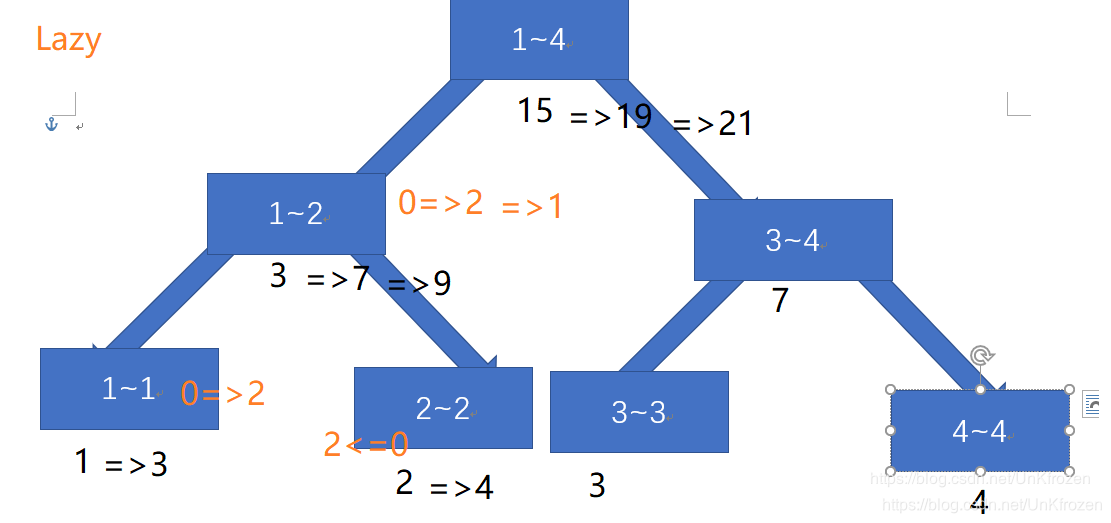
手搓大法好！！！

代码实现

0.核心代码 pushdown
1
2
3
4
5
6
7
8
9
10
void pushdown(Node p)
{
    if (p->lson != NULL) {  //如果该节点还有后续节点
        p->lson->lazy += p->lazy;  //令子节点lazy继承父节点lazy，下同
        p->lson->d += (p->lson->right - p->lson->left + 1)*p->lazy;  //修改子节点的值，下同
        p->rson->lazy += p->lazy;
        p->rson->d += (p->rson->right - p->rson->left + 1)*p->lazy;
    }
    p->lazy = 0; //令该节点的lazy清零
}
1.树本体
1
2
3
4
5
6
7
8
9
#ifndef NULL
#define NULL 0
#endif
typedef struct Segment_Tree* Node;
struct Segment_Tree {
    int d,lazy;   //仅仅多了一个lazy标记
    int left, right;
    Node lson, rson;
}*root;
2.建树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Node built(int left, int right)
{
    Node p = new(Segment_Tree);
    p->left = left;
    p->right = right;
    p->lazy = 0;  //只是对lazy标记进行初始化
    if (left == right) {
        p->d = a[left];
        p->lson = NULL;
        p->rson = NULL;
    }
    else {
        int mid = (left + right) / 2;
        p->lson = built(left, mid);
        p->rson = built(mid + 1, right);
        p->d = p->lson->d+p->rson->d;
    }
    return p;
}
void close(Node p)
{
    if (p != NULL) {
        close(p->lson);
        close(p->rson);
        delete(p); //free(p);c用法
    }
    return;
}
3.单点查询和单点修改无改变
4.区间查询
1
2
3
4
5
6
7
8
9
10
11
12
13
long long find(Node p, int x, int y)  //区间查询
{
    if (p->lazy != 0)  //解决一下历史遗留问题再查询
        pushdown(p);
    if (p->left == x && p->right == y)  //其他未变
        return p->d;
    int mid = (p->left + p->right) / 2;
    if (y <= mid)
        return find(p->lson, x, y);
    if (x > mid)
        return find(p->rson, x, y);
    return find(p->lson, x, mid)+find(p->rson, mid + 1, y);
}
5.区间修改
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int update(Node p, int x, int y, int k)  //区间修改
{
    if (p->lazy!=0)    //如果该节点的lazy不为零，就处理一下
            pushdown(p);
    if (p->left == x && p->right==y) {   //如果是要进行修改的节点，便让该节点的lazy为k，并修改值
        p->lazy = k;
        return p->d += k*(y - x + 1);
    }
    int mid = (p->left + p->right) / 2;
    if (y <= mid)
        return p->d = p->rson->d+update(p->lson, x, y, k);
    if (x > mid)
        return p->d = p->lson->d+ update(p->rson, x, y, k);
    return p->d = update(p->lson, x, mid, k) + update(p->rson, mid + 1, y, k);
}

（二）. 离散化

  离散化是一个听起来很高大上的方法.
  其实做起来很简单.当然如果想高深的话,自然也拦不住
  其实就是将一串数据储存到数组中,不将数据本身作为键值,而是选择使用数组的下标作为键值.
  形象的,$1,2,3,10000000$这四个数,保存在数组$a[]$中,相对应的下标为$1,2,3,4$就可以减少空间的开支.

数组实现

如果你觉得这个代码很熟悉!
那就当我抄的吧,嚯嚯嚯

洛谷线段树1:

戳我看代码~
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
#include <cstdio>
#include <cstdlib>
#include <iostream>
using namespace std;

const int MAXN = 100000 + 10;
typedef long long ll;
#define l(p) tree[p].lson
#define r(p) tree[p].rson

struct vec {
    ll d;
    int lson, rson;
    ll lazy;
    int L, R;
} tree[MAXN << 2];
int tot;
int rub()
{
    tot++;
    return tot;
}
void built(int& p, int l, int r)
{
    p = rub();
    tree[p].L = l, tree[p].R = r;
    tree[p].lazy = 0;
    if (l == r)
        cin >> tree[p].d;
    else {
        int mid = (l + r) >> 1;
        built(l(p), l, mid);
        built(r(p), mid + 1, r);
        tree[p].d = tree[l(p)].d + tree[r(p)].d;
    }
}
void pushdown(int p)
{
    if (l(p) && r(p)) {
        tree[l(p)].lazy += tree[p].lazy;
        tree[r(p)].lazy += tree[p].lazy;
        tree[l(p)].d += tree[p].lazy * (tree[l(p)].R - tree[l(p)].L + 1);
        tree[r(p)].d += tree[p].lazy * (tree[r(p)].R - tree[r(p)].L + 1);
    }
    tree[p].lazy = 0;
}

ll query(int p, int l, int r)
{
    pushdown(p);
    int L = tree[p].L, R = tree[p].R;
    if (L == l && R == r)
        return tree[p].d;
    int mid = (L + R) >> 1;
    if (l > mid)
        return query(r(p), l, r);
    else if (r <= mid)
        return query(l(p), l, r);
    return query(l(p), l, mid) + query(r(p), mid + 1, r);
}
void up(int p)
{
    tree[p].d = tree[l(p)].d + tree[r(p)].d;
}
void update(int p, int l, int r, ll k)
{
    pushdown(p);
    int L = tree[p].L, R = tree[p].R;
    if (L == l && r == R) {
        tree[p].d += k * (tree[p].R - tree[p].L + 1);
        tree[p].lazy += k;
        return;
    }
    int mid = (L + R) >> 1;
    if (l > mid)
        update(r(p), l, r, k);
    else if (r <= mid)
        update(l(p), l, r, k);
    else
        update(l(p), l, mid, k), update(r(p), mid + 1, r, k);
    up(p);
}
void print(int p)
{
    if (p == 0)
        return;
    pushdown(p);
    cout << p << ' ' << tree[p].L << ' ' << tree[p].R << ":" << tree[p].d << endl;
    print(l(p));
    print(r(p));
}
int main()
{
    int n, m;
    cin >> n >> m;
    int root;
    built(root, 1, n);
    while (m--) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) {
            ll k;
            cin >> k;
            update(root, x, y, k);
        } else
            cout << query(root, x, y) << endl;
    }
    return 0;
}

洛谷线段树2:

戳我看代码~
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
#include <cstdio>
#include <cstdlib>
#include <iostream>
using namespace std;

const int MAXN = 100000 + 10;
typedef long long ll;
#define l(p) tree[p].lson
#define r(p) tree[p].rson

struct vec {
    ll d;
    int lson, rson;
    ll add_lazy, mul_lazy;
    int L, R;
} tree[MAXN << 2];
int tot, mod;
int rub()
{
    tot++;
    return tot;
}
void built(int& p, int l, int r)
{
    p = rub();
    tree[p].L = l, tree[p].R = r;
    tree[p].add_lazy = 0;
    tree[p].mul_lazy = 1;
    if (l == r)
        cin >> tree[p].d;
    else {
        int mid = (l + r) >> 1;
        built(l(p), l, mid);
        built(r(p), mid + 1, r);
        tree[p].d = (tree[l(p)].d + tree[r(p)].d) % mod;
    }
}
void pushdown(int p)
{
    if (l(p) && r(p)) {
        tree[l(p)].add_lazy = tree[l(p)].add_lazy * tree[p].mul_lazy % mod;
        tree[r(p)].add_lazy = tree[r(p)].add_lazy * tree[p].mul_lazy % mod;
        tree[l(p)].mul_lazy = tree[l(p)].mul_lazy * tree[p].mul_lazy % mod;
        tree[r(p)].mul_lazy = tree[r(p)].mul_lazy * tree[p].mul_lazy % mod;
        tree[l(p)].add_lazy = (tree[l(p)].add_lazy + tree[p].add_lazy) % mod;
        tree[r(p)].add_lazy = (tree[r(p)].add_lazy + tree[p].add_lazy) % mod;
        tree[l(p)].d = (tree[l(p)].d * tree[p].mul_lazy + tree[p].add_lazy * (tree[l(p)].R - tree[l(p)].L + 1)) % mod;
        tree[r(p)].d = (tree[r(p)].d * tree[p].mul_lazy + tree[p].add_lazy * (tree[r(p)].R - tree[r(p)].L + 1)) % mod;
    }
    tree[p].add_lazy = 0;
    tree[p].mul_lazy = 1;
}

ll query(int p, int l, int r)
{
    pushdown(p);
    int L = tree[p].L, R = tree[p].R;
    if (L == l && R == r)
        return tree[p].d;
    int mid = (L + R) >> 1;
    if (l > mid)
        return query(r(p), l, r) % mod;
    else if (r <= mid)
        return query(l(p), l, r) % mod;
    return (query(l(p), l, mid) + query(r(p), mid + 1, r)) % mod;
}
void up(int p)
{
    tree[p].d = tree[l(p)].d + tree[r(p)].d;
}
void add_update(int p, int l, int r, ll k)
{
    pushdown(p);
    int L = tree[p].L, R = tree[p].R;
    if (L == l && r == R) {
        tree[p].d += k * (tree[p].R - tree[p].L + 1);
        tree[p].add_lazy += k;
        return;
    }
    int mid = (L + R) >> 1;
    if (l > mid)
        add_update(r(p), l, r, k);
    else if (r <= mid)
        add_update(l(p), l, r, k);
    else
        add_update(l(p), l, mid, k), add_update(r(p), mid + 1, r, k);
    up(p);
}
void mul_update(int p, int l, int r, ll k)
{
    pushdown(p);
    int L = tree[p].L, R = tree[p].R;
    if (L == l && r == R) {
        tree[p].d *= k;
        tree[p].add_lazy *= k;
        tree[p].mul_lazy *= k;
        return;
    }
    int mid = (L + R) >> 1;
    if (l > mid)
        mul_update(r(p), l, r, k);
    else if (r <= mid)
        mul_update(l(p), l, r, k);
    else
        mul_update(l(p), l, mid, k), mul_update(r(p), mid + 1, r, k);
    up(p);
}
void print(int p)
{
    if (p == 0)
        return;
    pushdown(p);
    cout << p << ' ' << tree[p].L << ' ' << tree[p].R << ":" << tree[p].d << endl;
    print(l(p));
    print(r(p));
}
int main()
{
    int n, m;
    cin >> n >> m >> mod;
    int root;
    built(root, 1, n);
    while (m--) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) {
            ll k;
            cin >> k;
            mul_update(root, x, y, k);
        } else if (op == 2) {
            ll k;
            cin >> k;
            add_update(root, x, y, k);
        } else
            cout << query(root, x, y) % mod << endl;
    }
    return 0;
}

练习题目

洛谷P2251
裸的RMQ问题,数据量小.
洛谷P3372
洛谷P3373
洛谷线段树模板题








 




 


 


 

 //删除Valine核心代码库外链调用 //调用刚下载的本地文件以加速加载速度 //这里改为从本地加载