参拜大佬%%%
二分图
定义
严格的定义请参加百度百科什么的.这里简单讲一下我的理解.就是给你一个图,有n个点.你可以按照边的关系,将这n个点分成两部分,而且这两部分之间有边相连.但是每一部分里面的点互不相连.
如图1,左右两部分的点随意相连,但是每部分里的每一个点互不相连.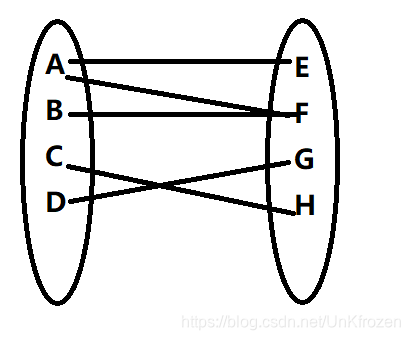
匹配
首先是极大匹配(Maximal Matching),是指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。
而最大匹配(maximum matching)是所有极大匹配当中边数最大的一个匹配。选择这样的边数最大的子集称为图的最大匹配问题。
如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配。
求二分图匹配可以用最大流(Maximal Flow)或者匈牙利算法(Hungarian Algorithm).
当然本蒟蒻还没有学最大流
匈牙利算法
我们来看图二,可以知道了这个二分图各点之间的联系.那么该算法如何实现最大匹配呢.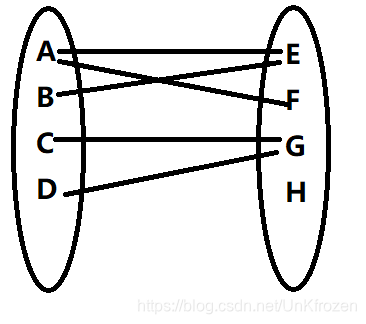
根据字典序,显然易见,我们可以知道,A->E.
随后,我们看B点,它要连E,但是E被占用了,我们该怎么办?我们把A->E之间的边暂时去掉,变成黄色,然后让B->E链接,但是A不能没有,于是这里从A再走,E不行,但是有个F.所以A->F.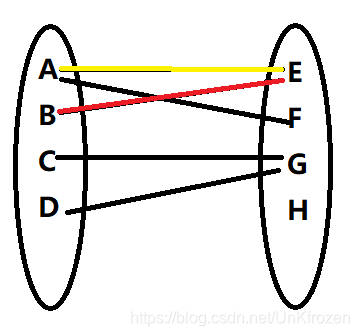
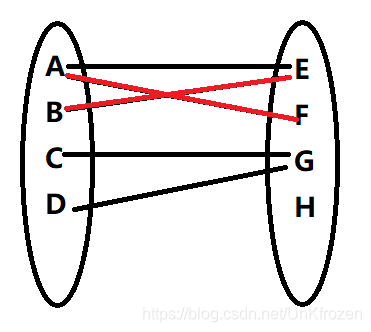
于是C->G也按此法加上,轮到D,我们发现G已经被连了.怎么办?将C->G的边暂时去掉.再从C走,看是否可以找别的边.但是我们发现,C只有到G的一条边.所以C->G保留,D只能孤立一人,我们无能为力.
核心代码
1 | bool find(int x) |
完整代码
1 |
|