高精度 | Kyons'Blog 


 




高精度

发表于 | 分类于 | | 阅读次数:

我好羡慕会用java的人

为什么要用到高精度呢?
我们知道,$int$的范围是$\pm2^{31}-1$,$long,long$的范围是$\pm2^{63}-1$,那么当我们想要表示更往上的数字,应该怎么做?
虽然,我已经学会了

我上小学

很计算机的一种方式,将每一位放在一个$a[i]$中,这样,一个数字就变成一个数组,对数字的四则运算,也就变成了对数组的操作.

高精度加法

问:$1234+5678$答案是多少?答:$我不知道$
咳咳,按照小学的教法,我们知道,要列个竖式,对齐数位,一位一位相加,满$10$进$1$.
于是:
$$\quad\quad1234\\underline{,\quad+5678}\\quad\quad6912$$
分析一下计算过程,我们发现,当我们用数组$a$,数组$b$,分别存下$1234$和$5678$后,从数组的最后一位开始$for$循环,用数组$S$保存和,$temp$保存进位
可以得到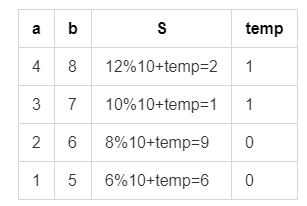

再将这个过程转化为代码,高精度加法就写出来了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
BigNum BigNum::operator+(const BigNum &i_T)const    //BigNum+BigNum
{
    BigNum t(*this);
    int big;
    big = i_T.len > len ? i_T.len : len;
    for (int i = 0; i < big; i++) {
        t.a[i] += i_T.a[i];
        if (t.a[i] > MAXN) {
            t.a[i + 1]++;
            t.a[i] -= MAXN + 1;
        }
    }
    t.len = (t.a[big] != 0) ? big + 1 : big;
    return t;
}

高精度减法

众所周知,减法是加法的逆运算.所以,我们将加法的过程反过来就是减法.

  1. 从头往后处理
  2. $temp$保存向后一位的借位
  3. 处理负数的偷懒方式为,将第一位前加个符号,输出的时候就加上了符号
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    BigNum BigNum::operator-(const BigNum &i_T)const //num - num
    {
        int big, j;
        bool flag;
        BigNum t1, t2;
        if (*this > i_T) {
            t1 = *this;
            t2 = i_T;
            flag = 0;
        }
        else {
            t1 = i_T;
            t2 = *this;
            flag = 1;
        }
        big = t1.len;
        for (int i = 0; i < big; i++) {
            if (t1. a[i] < t2.a[i]) {
                j = i + 1;
                while (t1.a[j] == 0)
                    j++;
                t1.a[j--]--;
                while (j > i)
                    t1.a[j--] += MAXN;
                t1.a[i] += MAXN + 1 - t2.a[i];
            }
            else
                t1.a[i] -= t2.a[i];
        }
        t1.len = big;
        while (t1.a[t1.len - 1] == 0 && t1.len > 1) {
            t1.len--;
            big--;
        }
        if (flag)
            t1.a[big - 1] = 0 - t1.a[big - 1];
        return t1;
    }

高精度乘法

我们现在还是小学
提问:$1234\times5678$答案是多少
我们来列个式杂
$\quad\quad\quad1234$
$;\quad\underline{\quad\times5678}$
$\quad\quad\quad9872$
$\quad\quad8638$
$\quad;;7404$
$\underline{\quad6170\quad;}$
$\quad7006652$
那么分析一下这个过程.
设一个空的$s$数组,$b$数组的个位$\times a$从个位开始和$s$的每一位相加,$b$数组的十位$\times a$从十位开始和$s$的每一位相加,以此类推,一直到$b$的千位计算结束,得到的便是答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
BigNum BigNum::operator*(const BigNum &i_T)const
{
    BigNum ret;
    int up, i=0, j=0, temp, temp1;
    for (i = 0; i < len; i++) {
        up = 0;
        for (j = 0; j < i_T.len; j++) {
            temp = a[i] * i_T.a[j] + ret.a[i + j] + up;
            if (temp > MAXN) {
                temp1 = temp - temp / (MAXN + 1)*(MAXN + 1);
                up = temp / (MAXN + 1);
                ret.a[i + j] = temp1;
            }
            else {
                up = 0;
                ret.a[i + j] = temp;
            }
        }
        if (up != 0)
            ret.a[i + j] = up;
    }
    ret.len = i + j;
    while (ret.a[ret.len - 1] == 0 && ret.len > 1)
        ret.len--;
    return ret;
}

高精度除法

好的,我们现在还是小学生

高精度除低精度

好的,首先,除法是乘法的逆元,所以我们~
倒着做回去

  1. 从头往后处理
  2. $down$储存余数
  3. 当余数+该位小于低精度的数时,我们向后延续一位
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    BigNum BigNum::operator/(const int &i_b)const
    {
        BigNum ret;
        int down = 0;
        for (int i = len - 1; i >= 0; i--) {
            ret.a[i] = (a[i] + down * (MAXN + 1)) / i_b;
            down = a[i] + down * (MAXN + 1) - ret.a[i] * i_b;
        }
        ret.len = len;
        while (ret.a[ret, len - 1] == 0 && ret.len > 1)
            ret.len--;
        return ret;
    }

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
#define MAXN 9999        //MAXN控制每个a[i]内大小
#define DLEN 4        //DLEN控制a[i]中有几位
#define MAXSIZE 5010    //控制数字位数

class BigNum {
private:
    int a[MAXSIZE];
    int len;
public:
    BigNum() {
        len = 1;
        memset(a, 0, sizeof(a));
    }
    BigNum(const int);
    BigNum(const char*);
    BigNum(const BigNum &);
    BigNum &operator=(const BigNum &);
    friend istream& operator>>(istream&, BigNum&);
    friend ostream& operator<<(ostream&, BigNum&);
    BigNum operator +(const BigNum &)const;
    BigNum operator -(const BigNum &)const;
    BigNum operator *(const BigNum &)const;
    BigNum operator /(const int &)const;
    BigNum operator ^(const int &)const;
    long long operator %(const long long &)const;
    bool operator >(const BigNum&i_T)const;
    bool operator >(const int &i_T)const;
    void print();
};

//int->BigNum
BigNum::BigNum(const int i_b)
{
    int c, d = i_b;
    len = 0;
    memset(a, 0, sizeof(a));
    while (d > MAXN) {
        c = d - (d / (MAXN + 1))*(MAXN + 1);
        d = d / (MAXN + 1);
        a[len++] = c;
    }
    a[len++] = d;
}
//char->BigNum
BigNum::BigNum(const char *i_s)
{
    int t, k, index, L;
    memset(a, 0, sizeof(a));
    L = strlen(i_s);
    len = L / DLEN;
    if (L%DLEN)
        len++;
    index = 0;
    for (int i = L - 1; i >= 0; i -= DLEN) {
        t = 0;
        k = i - DLEN + 1;
        if (k < 0)
            k = 0;
        for (int j = k; j <= i; j++)
            t = t * 10 + i_s[j] - '0';
        a[index++] = t;
    }
}
//copy
BigNum::BigNum(const BigNum &i_T) :len(i_T.len)
{
    memset(a, 0, sizeof(a));
    for (int i = 0; i < len; i++)
        a[i] = i_T.a[i];
}
//BigNum复制BigNum
BigNum&BigNum::operator=(const BigNum&i_n)
{
    len = i_n.len;
    memset(a, 0, sizeof(a));
    for (int i = 0; i < len; i++)
        a[i] = i_n.a[i];
    return *this;
}
//cin>> BigNum
istream& operator >>(istream &in, BigNum &i_b)
{
    char ch[MAXSIZE * DLEN];
    in >> ch;
    int L = strlen(ch), count = 0, sum = 0;
    for (int i = L - 1; i >= 0;) {
        sum = 0;
        int t = 1;
        for (int j = 0; j < DLEN && i >= 0; j++, i--, t *= 10)
            sum += (ch[i] - '0')*t;
        i_b.a[count] = sum;
        count++;
    }
    i_b.len = count++;
    return in;
}
//cout<<BigNum
ostream& operator <<(ostream& out, BigNum& i_b)
{
    cout << i_b.a[i_b.len - 1];
    for (int i = i_b.len - 2; i >= 0; i--)
        printf("%04d", i_b.a[i]);
    return out;
}
//高精度除低精度
BigNum BigNum::operator/(const int &i_b)const
{
    BigNum ret;
    int down = 0;
    for (int i = len - 1; i >= 0; i--) {
        ret.a[i] = (a[i] + down * (MAXN + 1)) / i_b;
        down = a[i] + down * (MAXN + 1) - ret.a[i] * i_b;
    }
    ret.len = len;
    while (ret.a[ret.len - 1] == 0 && ret.len > 1)
        ret.len--;
    return ret;
}
//高精度%低精度
long long BigNum::operator%(const long long &i_b)const
{
    long long d = 0;
    for (int i = len - 1; i >= 0; i--)
        d = ((d*MAXN + 1) % i_b + a[i] * 1LL) % i_b;
    return d;
}
//高精度求幂
BigNum BigNum::operator^(const int &n)const
{
    int i;
    BigNum t, ret(1);
    if (n < 0)
        exit(-1);
    if (n == 0)
        return 1;
    if (n == 1)
        return *this;
    int m = n;
    while (m > 1) {
        t = *this;
        for (i = 1; (i << 1) <= m; i <<= 1)
            t = t * t;
        m -= i;
        ret = ret * t;
        if (m == 1)
            ret = ret * (*this);
    }
    return ret;
}
//高精与高精比较
bool BigNum::operator>(const BigNum &i_T)const
{
    int ln;
    if (len > i_T.len)
        return true;
    else if (len < i_T.len)
        return false;
    else {
        ln = len - 1;
        while (a[ln] == i_T.a[ln] && ln > 0)
            ln--;
        return (ln >= 0 && a[ln] > i_T.a[ln]);
    }
}
//高精与低精度
bool BigNum::operator>(const int &i_T)const
{
    BigNum b(i_T);
    return *this > b;
}
//打印高精度
void BigNum::print()
{
    printf("%d", a[len - 1]);
    for (int i = len - 2; i >= 0; i--)
        printf("%04d", a[i]);
    printf("\n");
}
//高精度相乘
BigNum BigNum::operator*(const BigNum &i_T)const
{
    BigNum ret;
    int up, i=0, j=0, temp, temp1;
    for (i = 0; i < len; i++) {
        up = 0;
        for (j = 0; j < i_T.len; j++) {
            temp = a[i] * i_T.a[j] + ret.a[i + j] + up;
            if (temp > MAXN) {
                temp1 = temp - temp / (MAXN + 1)*(MAXN + 1);
                up = temp / (MAXN + 1);
                ret.a[i + j] = temp1;
            }
            else {
                up = 0;
                ret.a[i + j] = temp;
            }
        }
        if (up != 0)
            ret.a[i + j] = up;
    }
    ret.len = i + j;
    while (ret.a[ret.len - 1] == 0 && ret.len > 1)
        ret.len--;
    return ret;
}

BigNum BigNum::operator+(const BigNum &i_T)const    //BigNum+BigNum
{
    BigNum t(*this);
    int big;
    big = i_T.len > len ? i_T.len : len;
    for (int i = 0; i < big; i++) {
        t.a[i] += i_T.a[i];
        if (t.a[i] > MAXN) {
            t.a[i + 1]++;
            t.a[i] -= MAXN + 1;
        }
    }
    t.len = (t.a[big] != 0) ? big + 1 : big;
    return t;
}

BigNum BigNum::operator-(const BigNum &i_T)const //num - num
{
    int big, j;
    bool flag;
    BigNum t1, t2;
    if (*this > i_T) {
        t1 = *this;
        t2 = i_T;
        flag = 0;
    }
    else {
        t1 = i_T;
        t2 = *this;
        flag = 1;
    }
    big = t1.len;
    for (int i = 0; i < big; i++) {
        if (t1. a[i] < t2.a[i]) {
            j = i + 1;
            while (t1.a[j] == 0)
                j++;
            t1.a[j--]--;
            while (j > i)
                t1.a[j--] += MAXN;
            t1.a[i] += MAXN + 1 - t2.a[i];
        }
        else
            t1.a[i] -= t2.a[i];
    }
    t1.len = big;
    while (t1.a[t1.len - 1] == 0 && t1.len > 1) {
        t1.len--;
        big--;
    }
    if (flag)
        t1.a[big - 1] = 0 - t1.a[big - 1];
    return t1;
}

高精度除高精度

好的,我们现在不做小学生了
考虑用除低精度的做法,太麻烦了.
那么我们再回到那句话,除法是乘法的逆元.
考虑:
$a/b=c\ldots d$,那么也就意味着$d+c\times b=a$,那么只要找到一个数$c$,使得$c\times b+d=a$即可
于是,问题变为了加法和乘法的组合.
对于加法,一个个试的话,必定超时.
考虑两种方式:二分法和牛顿法.
高精度用不了牛顿法况且我也不会,使用二分法,复杂度为$O(logN)$.
对于乘法

  1. 普通的模拟$O(N^2)$.
  2. 分治乘法：最简单的是$Karatsuba$乘法，一般化以后有$Toom-Cook$乘法；
  3. 快速傅里叶变换$FFT$：（为了避免精度问题，可以改用快速数论变换$FNTT$），时间复杂度$O(N lgN lglgN)$。参照$Schönhage–Strassen algorithm$和$Fürer’s algorithm$
  4. 中国剩余定理：把每个数分解到一些互素的模上，然后每个同余方程对应乘起来就行

两者结合即可解决问题.
$fft$的话可以看一下$hdu1402$
$java$$AC$后,$c/c++$还在敲代码.








 




 


 


 

 //删除Valine核心代码库外链调用 //调用刚下载的本地文件以加速加载速度 //这里改为从本地加载