前向星

欢迎各大佬，大牛对本文指正，也希望本文能对各位有所帮助

一.基本概念

  前向星是什么??
  前向星是一个边集数组.啥玩意啊,拽什么专业词汇啊.也就是说,与邻接矩阵相比,前向星更像是用vector储存的邻接链表,是储存边的数组.
  这个数组储存的是图里的每一条边.(下面上图)
  下面是一组图的数据
  $4$个顶点,$6$条边,起点,终点,这条边的长度
4 6
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

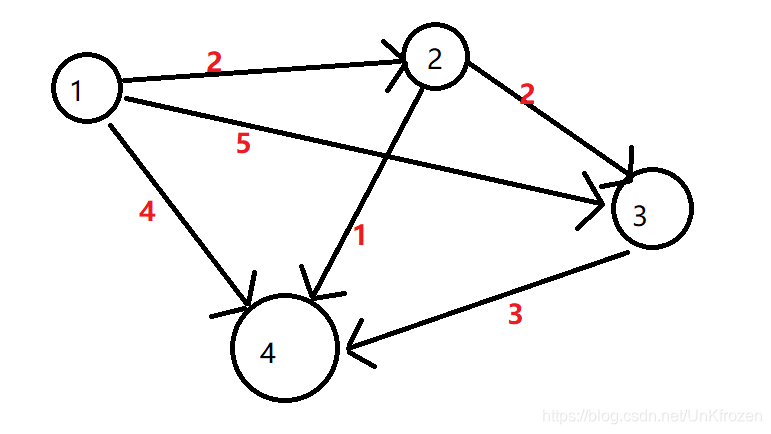
  前向星储存什么呢,存的是

第i条边	起点	终点	长度
1	1	2	2
2	2	3	2
3	2	4	1
4	1	3	5
5	3	4	3
6	1	4	4

二.代码实现

  看了一下存储方式是不是感觉so~~easy,确实如此.
  但是依然改变不了这是一个很优秀的数据结构(雾)

1.核心代码

struct edge {
    int star, end, cost;
}p[100000];

2.保存和输出

bool operator <(edge a, edge b)
{
    return a.star < b.star;
}
int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) 
        cin >> p[i].star >> p[i].end>>p[i].cost;
    sort(p, p + m);
    for (int i = 0; i < m; i++)
        printf("%d %d %d\n",p[i].star,p[i].end,p[i].cost);
    return 0;
}

  当一个巨大的图却只有几个边的时候,这种保存方式的优势就大大的体现了出来.但是储存后需要按照起点排序.才能进行搜索或者求最短路.
  于是复杂度就要加上了排序的耗时.

三.优化–链式前向星

1.基本概念

  没错,就是优化,让我们来考虑如何去掉这个鬼畜的排序$呢^呢$??
  只需要稍微改变一点点储存方式,再加入一个next就可以了.于是就像是从一个点发出去的链子一样.所以称为链式前向星(雾).
  怎么弄呢?
  $head[i]$保存的是第i个点的始边的位置,edge保存的是第i点的一条边的终点与长度,以及第i个点的下一条边的位置.分别用$end$,$cost$,$next$表示.
  于是就这样子了
  还是这个数据,会变成什么样子呢??

第i条边	起点	终点	长度
1	1	2	2
2	2	3	2
3	2	4	1
4	1	3	5
5	3	4	3
6	1	4	4

  使$next=0$表示木有出边 为什么边序号是倒着的??(这里先卖个关子,后面会说)

2.代码实现(边的储存以及输出)

(1).数组实现

struct edge {
    int end, cost,next;
}p[500001];
int head[10001];
int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int s,e, c;
        cin >> s >> e >> c;
        p[i].end = e, p[i].cost = c;
        p[i].next=head[s];
        head[s] = i;
    }
    for (int i = 1; i <= n; i++) {
        int f = head[i];
        while (f) {
            printf("%d %d %d\n", i, p[f].end, p[f].cost);
            f = p[f].next;
        }
    }
    return 0;
}

  为什么边的位置是倒着的,木措,就是因为这两行,保存方式为下图演示.

p[i].next=head[s];
head[s] = i;

  让$head[i]$储存输入的边的位置,再让这条边的指向变为$head[i]$储存的位置.那么就意味着,越晚输入的边,它越靠近$head[i]$.

(2).指针实现

  作为一个忠于指针写数据结构的人,怎么可能不用指针写一下这个家伙呢(雾).
  看懂上面的,这个应该没什么问题吧(逃)

typedef struct edge* nd;
struct edge {
    int end, cost;
    nd next;
};
nd head[10001];
void close(int n)
{
    for (int i = 1; i <= n; i++) {
        nd p = head[i];
        while (p != NULL) {
            nd f = p->next;
            delete(p);  //free(p);
            p = f;
        }
    }
}
    
int main()
{
    int n, m;
    cin >> n >> m;
    memset(head, NULL, sizeof(head));
    for (int i = 1; i <= m; i++) {
        int s, e, c;
        cin >> s >> e >> c;
        nd p = new(edge);    //nd p=(nd) malloc(sizeof(edge));
        p->end = e, p->cost = c;
        p->next = head[s];
        head[s] = p;
    }
    for (int i = 1; i <= n; i++) {
        nd f = head[i];
        while (f!=NULL) {
            printf("%d %d %d\n", i, f->end, f->cost);
            f = f->next;
        }
    }
    close(n);
    return 0;
}