前置知识
凸包
不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集中所有的点。
列如下图:用红色的直线,将黑色的点包裹起来.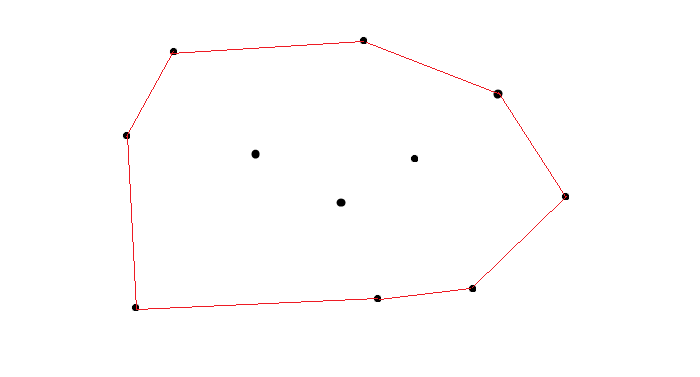
向量旋转
定义两个同一起点的向量:
分别为向量$\overrightarrow{ab}$和向量$\overrightarrow{ac}$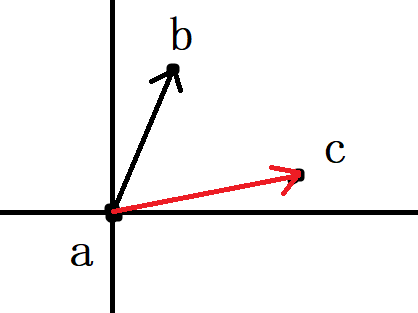
定义向量旋转,$\overrightarrow{ab}$旋转为$\overrightarrow{ac}$为右旋,即顺时针旋转.
$\overrightarrow{ac}$旋转为$\overrightarrow{ab}$为左旋,即逆时针旋转.
如何计算:
- 判断向量$\overrightarrow{ab}.x*\overrightarrow{ac}.y-\overrightarrow{ab}.y*\overrightarrow{ac}.x$的值.
- 若为正,则为$\overrightarrow{ab}$右旋变为$\overrightarrow{ac}$.
- 若为负,则为$\overrightarrow{ab}$左旋变为$\overrightarrow{ac}$.
- 若为$0$,则为共线.
正题
前篇
我们知道,一个凸包,它要包含所有点集中的点.
那么如图: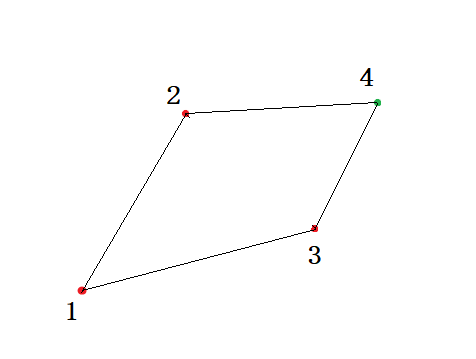
为了符合凸包定义,只有$1,2,3,4$四点时,我们的凸包如图所示(在这里,我们假设所有的点按照$x$从小到大给出)
那么,对于第$5$个点,我们应该怎么处理呢?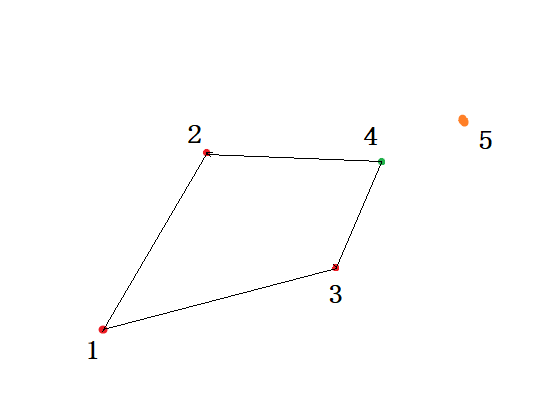
- 边$2\rightarrow4$应该断开,然后将$2\rightarrow5$连接
- 再将$3\rightarrow4$断开.然后将$3\rightarrow5$连接
变成这样: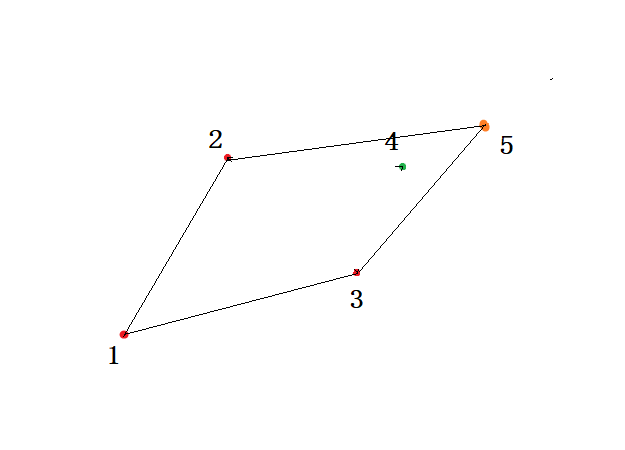
我们可以简单把这个凸包划分为上半部分和下半部分.
- 对于上半部分的$1,2,4,5$
- 为什么断开$2\rightarrow4$而连接$2\rightarrow5$?
- 因为$4$在$2\rightarrow5$的内侧?
- 这是一个原因,但本质是
- 向量$\overrightarrow{2\rightarrow4}$是需要左旋才能成为$\overrightarrow{2\rightarrow5}$
- 同理可以得到,对于$3\rightarrow4$变$3\rightarrow5$
- 向量$\overrightarrow{3\rightarrow4}$是需要右旋才能成为$\overrightarrow{3\rightarrow5}$
中篇
由上面得到的这条性质.
我们能做什么?
- 在离线,所给的点集无序时,我们有了$O(n\log{n})$的算法.
- 当所给的点集是有序时,我们有$O(n)$的算法.
后篇
我们分为两种类型进行讨论.
有序的且符合简单多边形的点集
什么是简单多边形?
- 顶点与顶点不重合。
- 顶点不在边上。
- 边与边不相交的多边形。
有序是什么?
- 按照$X$,$Y$坐标排序的有序
- 按照逆时针或顺时针给出的有序,当然也阔以称之为极角排序的有序.
首先先看第一种排序,按照逆时针或顺时针给出的有序,(极角排序的有序).
当仁不让$Graham$算法
- 算法思路:
- 1.栈名$q$,栈尾指针$tail$,初始化在栈中加入最左下角的点,和第二个点
- 2.假设即将加入的点$c$
- 3.判断向量$\overrightarrow{q_{tail-1}q_{tail}}$和向量$\overrightarrow{q_{tail-1}c}$的旋转关系.
- 1).如果是$\overrightarrow{q_{tail-1}q_{tail}}$右旋变为$\overrightarrow{q_{tail-1}c}$,将栈顶元素$q_{tail}$弹出,进行步骤$3$,直到进行步骤$2)$不成立或栈内只剩$2$个元素.
- 2).如果是$\overrightarrow{q_{tail-1}q_{tail}}$左旋变为$\overrightarrow{q_{tail-1}c}$,将$c$压入栈,回到步骤$2$.
- 如果发现三点共线的情况,算法可以考虑将其视为左转或者右转。这取决于究竟只是要求凸包的边界,还是要找到在凸包边界上所有的点。
- 示意图:
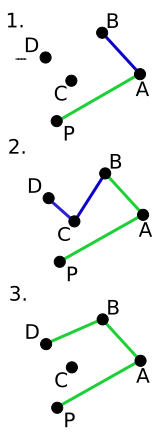
- 算法思路:
被大家吹的很厉害的$Melkman$算法
援引一下$Melkman$在论文中说的:
It is the purpose of this short article to show that a slightly modified version of their algorithm constructs, on-line, the convex hull of any simple polyline in $O(n)$ time.
在论文中,$Melkman$使用的是:顺时针.
当然,逆时针也阔以.
算法思路:
- 根据简单多边形的性质,我们知道边和边是不相交的.
- 1.确立一条边,使其他所有的点都在这条边的一侧
- 2.在一个双端队列的队尾放入边的两点,
- 3.再在队列头和尾都放入第三个点.
- 4.依次读入每一个点$p$,并与$q_{tail},q_{tail-1},q_{head},q_{head+1}$比较.
- 1).如果是$\overrightarrow{q_{tail-1}q_{tail}}$右旋变为$\overrightarrow{q_{tail-1}p}$,将队尾元素$q_{tail}$弹出,进行步骤$4$,直到进行步骤$1)$不成立或栈内只剩$3$个元素.
- 2).如果是$\overrightarrow{q_{tail-1}q_{tail}}$左旋变为$\overrightarrow{q_{tail-1}c}$,将$c$压入队尾,回到步骤$3$.
- 3).如果是$\overrightarrow{q_{head+1}q_{head}}$右旋变为$\overrightarrow{q_{head+1}p}$,将队首元素$q_{head}$弹出,进行步骤$4$,直到进行步骤$3)$不成立或队内只剩$3$个元素.
- 4).如果是$\overrightarrow{q_{head+1}q_{head}}$左旋变为$\overrightarrow{q_{head+1}p}$,将$p$压入队尾,回到步骤$3$.
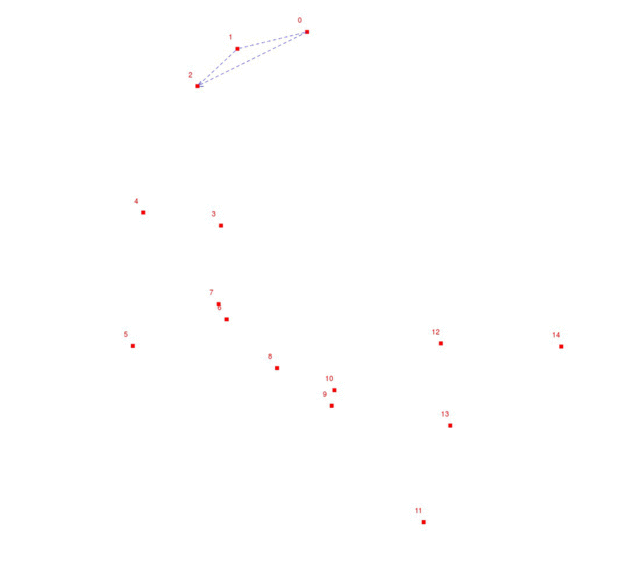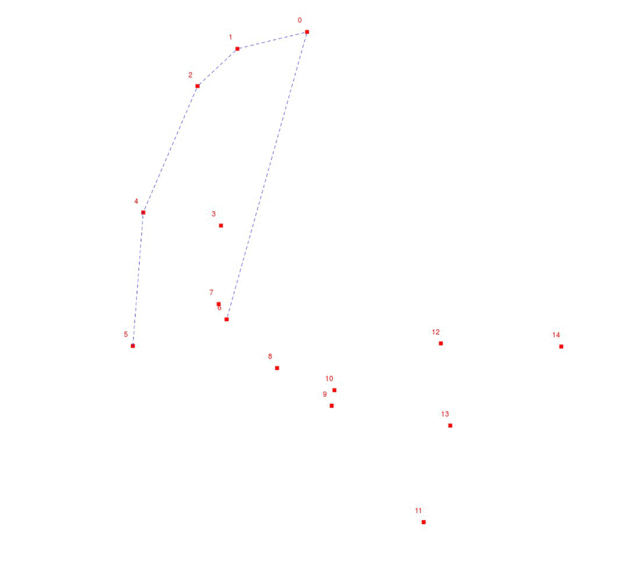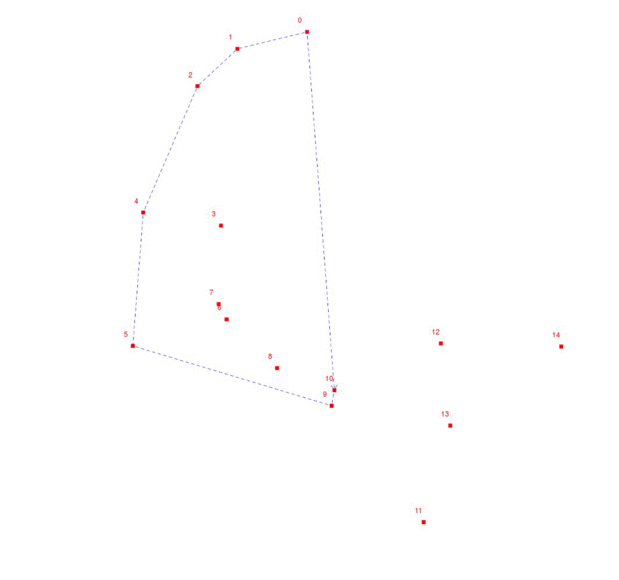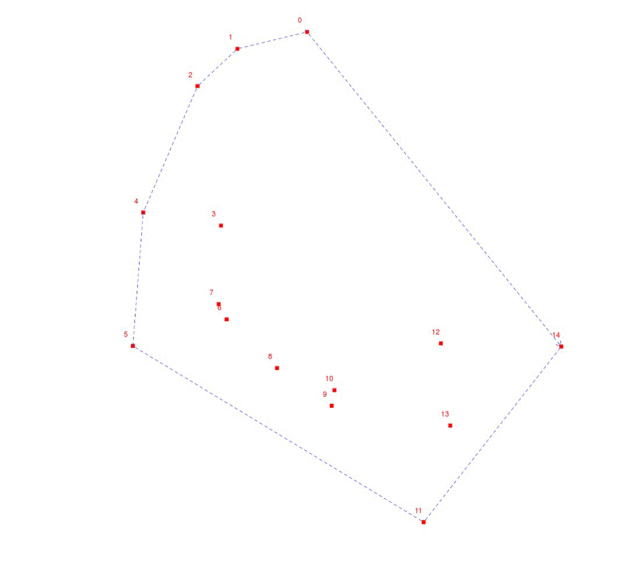
我们来进一步理解这个算法
- 看图
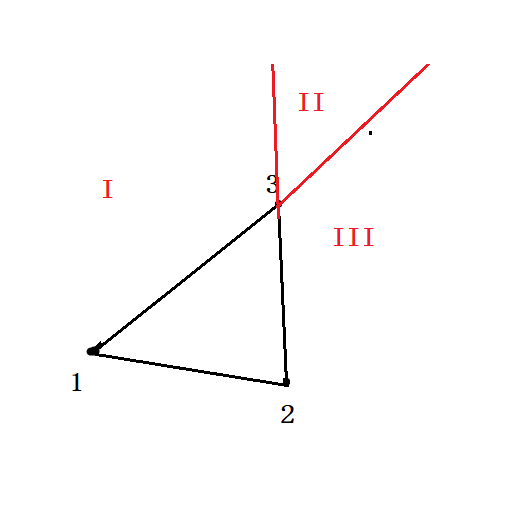
- 因为所给的点是有序的,那么点只能落在$I,II,III$这三个位置.
- 在这里,我们的$q[head]$和$q[tail]$都是$3$.
- 加入点$4$便判断,在$I$,那么$head++$,然后压入$4$
- 若在$III$,那么$tail–$,压入$4$.
- 若在$II$,则$head++,tail–$,再分别压入$4$.
- 重复上述步骤,直到所有点遍历结束.
- 看图
对于数据是按$x$从小到大,$x$相等时$y$从小到大的排列的点集
- 升级版的$Graham$算法:$Andrew$算法
- 当使用极角排序时的精度丢失又是一个折磨人的事情.
- 对于$Graham$算法,对于判断三点共线时有可能出现错误:
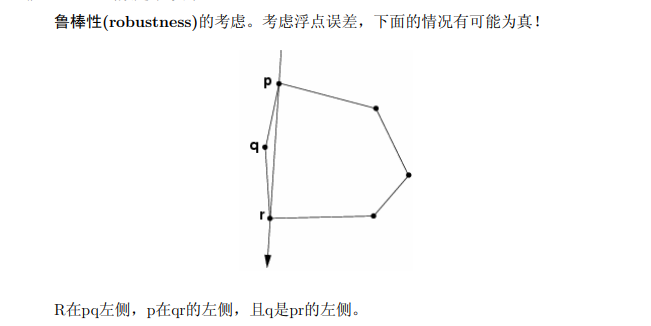
- 算法思路:
- 我们结合$Graham$来看.
- 在$Andrew$算法中,数据要按照$x$坐标来排列.
- 之后,先从点$1$扫到$n$,按照$Gramham$的处理,得到上凸包
- 再从$n$扫到$1$,得到下凸包,结束.
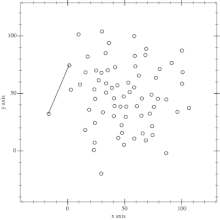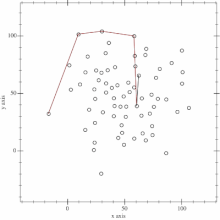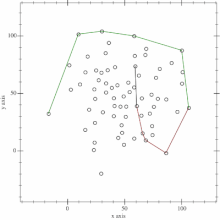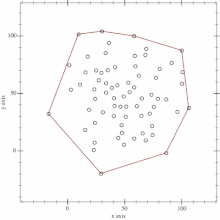
- 升级版的$Graham$算法:$Andrew$算法
无序的点集
其实理解了上面有序的点集如何求解,无序的点集也就非常明了了.
对于:$Graham$算法和$Melkman$算法,我们需要按照极角排序.
对于:$Andrew$算法,我们要按照$x$从小到大的顺序排列.
也就是说,目前,据我所知,对于无序的点集,我们都需要$O(n\log n)$的时间寻找凸包.
代码
$Graham$算法
1 | double Cross(vec A, vec B) |
$Andrew$算法
1 | double Cross(vec A, vec B) |