acm2014-I.The Queen’s Super-circular Patio

I: The Queen’s Super-circular Patio

题目描述

The queen wishes to build a patio paved with of a circular center stone surrounded by circular rings of circular stones. All the stones in a ring will be the same size with the same number of stones in each ring. The stones in the innermost ring will be placed touching (tangent to) the adjacent stones in the ring and the central stone. The stones in the other rings will touch the two adjacent stones in the next inner ring and their neighbors in the same ring. The figures below depict a patio with one ring of three stones and a patio with $5$ rings of $11$ stones. The patio is to be surrounded by a fence that goes around the outermost stones and straight between them (the heavier line in the figures).

The queen does not yet know how many stones there will be in each circle nor how many circles of stones there will be. To be prepared for whatever she decides, write a program to calculate the sizes of the stones in each circle and the length of the surrounding fence. The radius of the central stone is to be one queenly foot.

输入

The first line of input contains a single integer $P$, ($1 ≤ P ≤ 1000$), which is the number of data sets that follow. Each data set should be processed identically and independently.
Each data set consists of a single line of input. It contains the data set number, $K$, the number, $N$ ($3 ≤ N ≤ 20$), of stsones in each circle and the number, $M$ ($1 ≤ M ≤ 15$), of circles of stones around the central stone.

输出

For each data set there is a single line of output. It contains the data set number, $K$, followed by a single space which is then followed by the radius (in queenly feet) of the stones in the outermost ring (to $3$ decimal places) which is followed by a single space which is then followed by the length (in queenly feet) of the fence (to $3$ decimal places).

样例输入

3
1 3 1
2 7 3
3 11 5

样例输出

1 6.464 79.400
2 3.834 77.760
3 2.916 82.481

解析

$t$组数据,第一个是编号,第二个是一层有几个,第三个是有几层.
问你最外层的圆的半径$r$和围栏长度$l$.
首先,最外围的围栏长度$l$必定是最外围$1$个圆的周长$+n\times 2\times$最外围圆的半径$r$.
那么问题变为如何求最外围圆的半径$r$.
对于第一个图,很明显,最外层,即第一层的半径为$\frac{\sin\theta}{(1.0 - \sin\theta)}$,这里$\theta=\frac{\pi}{n}$
就像这样,理解一下.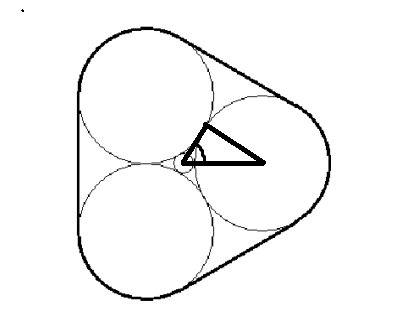

我们改一下图,让第二个图只有两层
那么问题变为如何求$r_2$.
我们连接两球的圆心,外切圆和外切圆的外切圆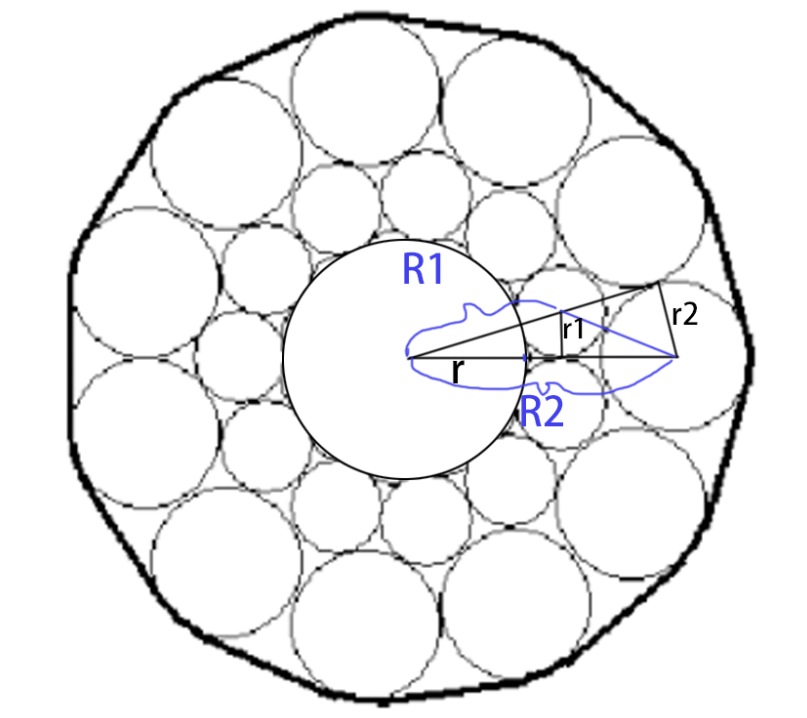

由$r_1=R_1\times\sin\theta,r_2=R_2\times\sin\theta$我们可以得到一个公式: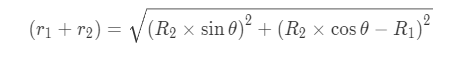

一系列化简得到

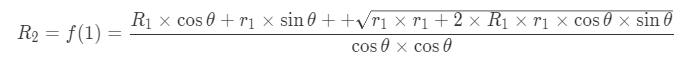
$$r_2=R_2*\sin\theta$$

之后每个$R_i=f(i-1)$递推求得.

int main()
{
    int t;
    cin >> t;
    while (t--) {
        int opt, n, k;
        cin >> opt >> n >> k;
        double alpha = pi / (double)n;
        double si=sin(alpha),ci=cos(alpha),ti=tan(alpha);
        double r1 = si / (1.0 - si);
        double R1=1.0+r1,R2,r2;
        for (int i = 2; i <= k; i++) {
            R2=R1*ci+r1*si+sqrt(r1*r1+2*r1*R1*ci*si);
            R2=R2/(ci*ci);

            r2=R2*si;
            R1=R2;
            r1=r2;
        }
        double r=r1;
        double ans=2.0*r*(pi+(double)(n));
        printf("%d %.3f %.3f\n", opt, r, ans);
    }
    return 0;
}