HDU6603 Azshara's deep sea

题目大意

题目很长，是有关于WOW的一个攻略出的模拟题。
大致意思就是
给你一堆点和一堆圆，问你在符合题意下，最多能连几条线段。
要求如下：

线段不能相交，端点重合除外
线段不能与圆相交或相切
线段两个端点不能相邻，如$(i,i+1)$ 或$(i-1,i)$
端点必须最靠外

根据这四条要求,就可以做了…

思路

首先，端点必须最靠外，就是说端点是凸包上的点。就是说，先跑个凸包。
其次，线段两个端点不相邻，且不与圆相交或相切，枚举一遍就好了。
最后，考虑线段不相交。线段端点都是凸包上的点，那么只要满足，线段$ab$和线段$cd$，$c<a\&\&b<d$即可。
如图1：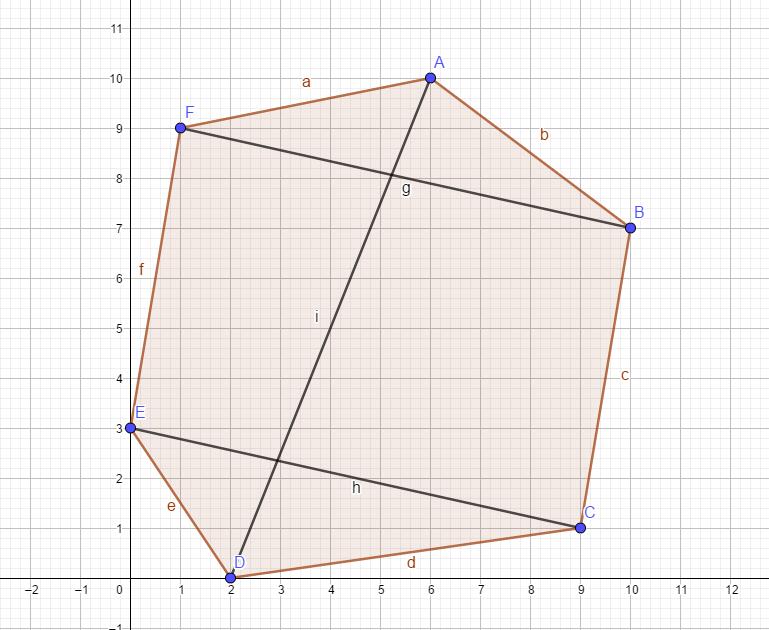

因此题目变成了，求最大线段不相交数量。嗯，显然dp。
然后考虑上面凸包线段不相交的性质，是一种包含关系。可以得出，这是一个区间dp。
然后就是，枚举小区间，再求大区间了。
$dp[i][j]=max(dp[i][j],dp[i][t]+dp[t][j]+dk[i][j]);$
其中，$dk$指的是该线段是否是符合$2$，$3$，$4$的，符合为$1$，不符合为$0$

代码

代码如下

/*
#pragma comment(linker, "/STACK:102400000,102400000")
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
#include <ext/pb_ds/priority_queue.hpp>
using namespace __gnu_pbds;
*/
#include <algorithm>
#include <bitset>
#include <cmath>
#include <iostream>
#include <string.h>
#include <vector>

using namespace std;
#define inf __INT_MAX__
#define enf INT_MIN
#define INF LLONG_MAX
#define ENF LLONG_MIN
const int MAXN = 1e3 + 10;
const double pi = acos(-1.0);
const double eps = 1e-6;
typedef long long ll;
#define zhengfu(x) ((x > eps) - (x < -eps))

typedef struct point vec;
struct point { //点的基本数据结构
    double x, y;
    double poe;
    point(double _x = 0, double _y = 0)
        : x(_x), y(_y) {
    }
    double len() //模长
    {
        return sqrt(x * x + y * y);
    }
    vec chuizhi() {
        return vec(-y, x);
    }
    double operator*(const point &i_T) const //点积
    {
        return x * i_T.x + y * i_T.y;
    }
    double operator^(const point &i_T) const //叉积
    {
        return x * i_T.y - y * i_T.x;
    }
    point operator*(double u) const {
        return point(x * u, y * u);
    }
    bool operator==(const point &i_T) const {
        return fabs(x - i_T.x) < eps && fabs(y - i_T.y) < eps;
    }
    point operator/(double u) const {
        return point(x / u, y / u);
    }
    point operator+(const point &i_T) {
        return point(x + i_T.x, y + i_T.y);
    }
    point operator-(const point &i_T) {
        return point(x - i_T.x, y - i_T.y);
    }
    friend bool operator<(point a, point b) {
        return fabs(a.y - b.y) < eps ? a.x < b.x : a.y < b.y;
    }
    void atn2() {
        poe = atan2(y, x);
    }
    friend ostream &operator<<(ostream &out, point &a) {
        //cout << a.x << ' ' << a.y;
        printf("%.8f %.8f", a.x, a.y);
        return out;
    }
    friend istream &operator>>(istream &in, point &a) {
        scanf("%lf%lf", &a.x, &a.y);
        return in;
    }
};
struct cirles {
    point o;
    double r;
    cirles(point _o = point(), double _r = 0.0)
        : r(_r), o(_o) {
    }
    point Point(double t) //圆上任意一点
    {
        return point(o.x + r * cos(t), o.y + r * sin(t));
    }
    friend istream &operator>>(istream &in, cirles &a) {
        in >> a.o >> a.r;
        return in;
    }
    friend ostream &operator<<(ostream &out, cirles &a) {
        out << a.o << ' ';
        printf("%.8f", a.r);
        return out;
    }
};
typedef struct Line Segment; //线段Segment
struct Line {                //直线
    point a, b;
    double poe;
    Line(point _a = point(), point _b = point())
        : a(_a), b(_b) {
    }
    double len() {
        return (a - b).len();
    }
    bool in(point pi) {
        if (b < a)
            return ((b == pi || b < pi) && (a == pi || pi < a));
        return ((a == pi || a < pi) && (b == pi || pi < b));
    }
    friend istream &operator>>(istream &in, Line &a) {
        cin >> a.a >> a.b;
        return in;
    }
    friend ostream &operator<<(ostream &out, Line &a) {
        out << a.a << ' ' << a.b;
        return out;
    }
    void atn2() {
        poe = atan2(b.y - a.y, b.x - a.x);
    }
};
double xuanzhuan(vec a, vec b, vec c) //求三点叉积，正为(b-a)->(c-a)左旋
{
    return (b - a) ^ (c - a);
}
void Andrew(point po[], int n, point qo[], int &tail) //求凸包,<0则包含凸包边上的点,<=0则只输出拐点
{
    sort(po + 1, po + 1 + n);
    tail = 1;
    qo[1] = po[1];
    for (int i = 2; i <= n; i++) {
        while (tail > 1 && xuanzhuan(qo[tail - 1], qo[tail], po[i]) <= 0)
            tail--;
        qo[++tail] = po[i];
    }
    int basic = tail;
    for (int i = n - 1; i >= 1; i--) {
        while (tail > basic && xuanzhuan(qo[tail - 1], qo[tail], po[i]) <= 0)
            tail--;
        qo[++tail] = po[i];
    }
}
double zhixian_yuanxin_juli(Line l, cirles a) //直线到圆心的距离
{
    return fabs((a.o - l.a) ^ (l.b - l.a)) / (l.b - l.a).len();
}
bool check(Segment si, cirles ci[], int g) {
    for (int i = 1; i <= g; i++)
        if (zhixian_yuanxin_juli(si, ci[i]) <= ci[i].r)
            return false;
    return true;
}
point p[MAXN], q[MAXN];
cirles c[MAXN];
int dk[MAXN][MAXN], dp[MAXN][MAXN];
int main() {
    int t;
    cin >> t;
    while (t--) {
        int n, g, r;
        cin >> n >> g >> r;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                dp[i][j] = dk[i][j] = 0;
        for (int i = 1; i <= n; i++)
            cin >> p[i];
        for (int i = 1; i <= g; i++) {
            cin >> c[i].o;
            c[i].r = r;
        }
        int tail;
        Andrew(p, n, q, tail);
        for (int i = 1; i < tail; i++)
            for (int j = i + 2; j < tail - (i == 1); j++)
                if (check(Segment(q[i], q[j]), c, g))
                    dk[i][j] = 1;
        for (int k = 2; k <= n; k++)
            for (int i = 1; i <= n - k; i++) {
                int j = i + k;
                for (int t = i + 1; t < j; t++)
                    dp[i][j] = max(dp[i][j], dp[i][t] + dp[t][j] + dk[i][j]);
            }
        int ans = enf;
        for (int i = 1; i < tail; i++)
            for (int j = i + 2; j < tail - (i == 1); j++)
                ans = max(ans, dp[i][j]);
        cout << ans << endl;
    }
    return 0;
}
/*
1
5 3 1
6 10
10 7
9 1
2 0
0 3
2 2
5 6
8 3
*/